Step-by-step explanation:
We will calculate the density as follows.
n =
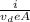
As the metallic wire is in the shape of a circle. So, its area will be calculated as follows.
Area =

=

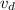 =
=
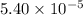
i = 8 A
Hence, we will calculate the density of free electrons as follows.
n =
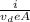
=
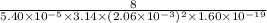
=
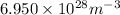
Thus, we can conclude that the density of free electrons in the metal is
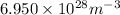 .
.