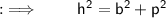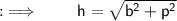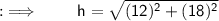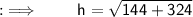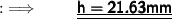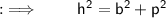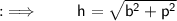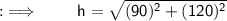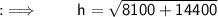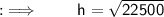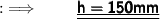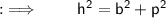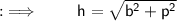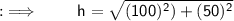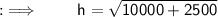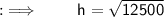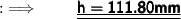Answers:
➝ Hypotenuse of triangle ( a ) = 21.63 mm
➝ Hypotenuse of triangle ( b ) = 150 mm
➝ Hypotenuse of triangle ( c ) = 111.80 mm

Solution:
We have to find the length of hypotenuse in the given 3 triangles, which can be done by using Pythagoras theorem.
- Pythagoras theorem states that :
" In a right angled triangle, the square of hypotenuse side is equal to the sum of square of other two sides "
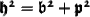
And we have to convert the answer to the units indicated in red i.e, in mm.
Since 1cm = 10 mm, we will convert the given values of length of side in mm before putting the values in the formula