Answer:
See below ↓
Explanation:
We need to prove :
⇒ cos⁻¹
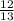 + sin⁻¹
+ sin⁻¹
 = tan⁻¹
= tan⁻¹
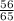
Let's simplify the LHS.
- cos⁻¹
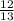 + sin⁻¹
+ sin⁻¹

Convert the inverse cos and sin functions into inverse tan functions
- tan⁻¹
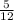 + tan⁻¹
+ tan⁻¹
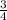
- [∴This can be found taking a right triangle and labeling the sides, and then using Pythagorean Theorem, we can find the missing side and take the ratio of tan]
Identity
- tan⁻¹ x + tan⁻¹ y = tan⁻¹
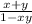
Using this identity, we can simplify our earlier equation!
⇒ tan⁻¹ [(5/12 + 3/4)/(1 - (5/12 x 3/4))]
⇒ tan⁻¹ [(20 + 36) / (48 - 15)
⇒ tan⁻¹ (56/65)
⇒ RHS
⇒ Proved ∴√