Question

There also was an exponentially-growing population of anteaters on board. At the start of the voyage there were 17 anteaters, and the population of anteaters doubled every 3.6 weeks. How long into the voyage were there 200 ants per anteater? (Round your answer to one decimal place.)

Answer 1

there will be 200 ants per anteater after 5.78 weeks.

Step-by-step explanation:

As the question is not complete, the first part is missing from which the population of ants at any given time is calculated as
`y=400e^(0.56t)`.

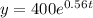At the start t=0, y=17

now the equation of population is given as

`y=a_1e^(b_1t)`

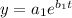
Here a1=17 for calculation of b1 using the doubling time of 3.6 weeks.

`y=a_1e^(b_1t)\\34=17e^(b_1*3.6)\\2=e^(b_1*3.6)\\b_1=ln(2)/3.6\\b_1=0.1925 week^(-1)`

So the equation is given as
`y=17e^(0.19t)`

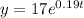
Now by using the equation

`(200)/(1)=(400e^(0.56t))/(17e^(0.19t))\\200*17=400e^(0.56t-0.19t)\\t=(\ln \left((17)/(2)\right)\cdot \:100)/(37)\\t=5.78`

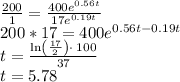
So there will be 200 ants per anteater after 5.78 weeks.