Answer:
d. 0V
Step-by-step explanation:
The magnitude of four point charges are +3q, -q, +2q and -4q. I think you forget to mention the signs.
As we know that the potential due to the point charge that has traveled the distance d can be represented mathematically as,
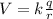
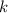 = 1/4λε = 9×
= 1/4λε = 9×
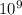 Nm²/C²
Nm²/C²
Now as it is mentioned in the question that all four charges are arranged in the corners of a square so there distance from the center is same. We can rewrite the above potential equation as follows.
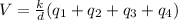 (1)
(1)
We can find out d by the pythagoras theorem, as we are dealing with square so d is a semi diagonal.
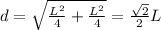
by putting all values in equation (1)
V =
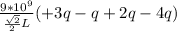
V = 0V