Question

Four point charges of magnitudes 3q q 2q and 4q are arranged in the corners of a square of side length L.The charge q creates a potential of 1 V relative to infinity in the center of the square.

What is the total potential created in the center of a square by all 4 charges?

a. 1V
b. 10V
c. It is impossible to determine without knowing the exact arrangement.
d. 0V
e. 5V

Answer 1

d. 0V

Step-by-step explanation:

The magnitude of four point charges are +3q, -q, +2q and -4q. I think you forget to mention the signs.

As we know that the potential due to the point charge that has traveled the distance d can be represented mathematically as,

`V = k(q)/(r)`

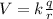
`k` = 1/4λε = 9×
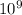`10^(9)` Nm²/C²

Now as it is mentioned in the question that all four charges are arranged in the corners of a square so there distance from the center is same. We can rewrite the above potential equation as follows.

`V = (k)/(d) (q_(1) + q_(2) +q_(3) +q_(4) )` (1)

We can find out d by the pythagoras theorem, as we are dealing with square so d is a semi diagonal.

`d = \sqrt{(L^(2) )/(4)+(L^(2) )/(4) } = (√(2) )/(2) L`

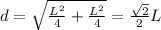
by putting all values in equation (1)

V =
`(9*10^(9) )/((√(2) )/(2) L ) (+3q-q+2q-4q)`

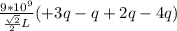
V = 0V