Question

An air force intercept squadron consists of 16 planes that should always be ready for immediate launch. However, a plane's engine can be troublesome, and there is a probability of .25 that the engines of a particular plane will not start at a given attempt. if this happens, the mechanic ,must wait 5 minutes before trying to start with the engines again. The squadron commander is interested in how many planes will immediately become airborne if the squadron is scrambled. Find the expected number of planes that would be successfully launched (the mean), the variance, the standard deviation, the probability that exactly 12 planes scramble successfully and the probability that at least 14 planes scramble successfully.

Answer 1

(a) The mean, variance and standard deviation of planes that would be successfully launched are 12, 3 and 1.732 respectively.

(b) The probability that exactly 12 planes scramble successfully is 0.225.

(c) The probability that at least 14 planes scramble successfully is 0.1971.

Explanation:

Let X = number of planes whose engines will start at the first attempt.

The probability of X is:

P (A plane starting immediately) = 1 - P (A plane not starting at the 1st attempt)

= 1 - 0.25

p = 0.75

The number of planes at the air force intercept squadron is, n = 16.

The random variable X follows a Binomial distribution, i.e.
`X\sim Bin(16,0.75)`

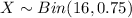
(a)

The expected value of a Binomial distribution is:

`E(X)=np`

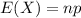
Compute the expected number of planes that would be successfully launched as follows:

`E(X)=np=16*0.75=12`

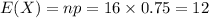
The variance of a Binomial distribution is:

`V(X)=np(1-p)`

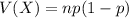
Compute the variance of planes that would be successfully launched as follows:

`V(X)=np(1-p)=16*0.75* (1-0.75)=3`

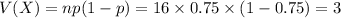
Compute the standard deviation of planes that would be successfully launched as follows:

`SD(X)=√(V(X))=√(3)=1.732`

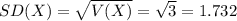
Thus, the mean, variance and standard deviation of planes that would be successfully launched are 12, 3 and 1.732 respectively.

(b)

The probability function of a Binomial distribution is:

`P(X=x)={n\choose x}p^(x)(1-p)^(n-x)`

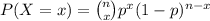
Compute the probability that exactly 12 planes scramble successfully as follows:

`P(X=12)={16\choose 12}(0.75)^(12)(1-0.75)^(16-12)=1820*0.0317*0.0039=0.225`

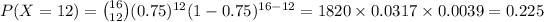
Thus, the probability that exactly 12 planes scramble successfully is 0.225.

(c)

Compute the probability that at least 14 planes scramble successfully as follows:

P (X ≥ 14) = P (X = 14) + P (X = 15) + P (X = 16)

`={16\choose 14}(0.75)^(14)(1-0.75)^(16-14)+{16\choose 15}(0.75)^(15)(1-0.75)^(16-15)\\+{16\choose 16}(0.75)^(16)(1-0.75)^(16-16)\\=0.1336+0.0535+0.01\\=0.1971`

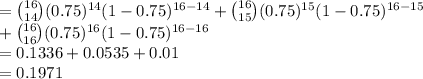
Thus, the probability that at least 14 planes scramble successfully is 0.1971.