Question

The grades on a physics midterm at Covington have an average of μ=72 and σ=2.0 If Stephanie scored 1.23 standard deviations above the mean.

a. What score did Stephanie get on the exam?
b. What percent of students scored better than Stephanie?

Answer 1

a) She scored 74.46 on the exam.

b) 11% of the students scored better than Stephanie.

Explanation:

The z-score measures how many standard deviation a score X is above or below the mean. It is given by the following formula:

`Z = (X - \mu)/(\sigma)`

In which
`\mu` is the mean and
`\sigma` is the standard deviation.

In this problem, we have that:

`\mu = 72, \sigma = 2`

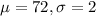
a. What score did Stephanie get on the exam?

Stephanie scored 1.23 standard deviations above the mean. This means that her z-score is
`Z = 1.23`

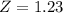
We want to find X

`Z = (X - \mu)/(\sigma)`

`1.23 = (X - 72)/(2)`

`X - 72 = 2*1.23`

`X = 74.46`

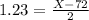
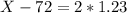
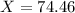
She scored 74.46 on the exam.

b. What percent of students scored better than Stephanie?

Each z-score has a pvalue, which is the percentile of the score. We look this pvalue at the z table.

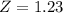`Z = 1.23` has a pvalue of 0.89.

This means that Stephanie's score is in the 89th percentile, which means that she scored more than 89% of the students and scored less than 100-89 = 11% of the students.

So 11% of the students scored better than Stephanie.