Question

Given the equation of a circle, x^2 + y^2 - 6x + 2y + 1 = 0, find the coordinates of the center and the length of the radius

Answer 1

Center: (3,-1)

Radius: 3

Explanation:

Given:

`\displaystyle \large{x^2+y^2-6x+2y+1=0}`

First, we have to convert the following standard circle equation to this:

`\displaystyle \large{(x-h)^2+(y-k)^2=r^2}`

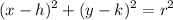
where h is horizontal shift, k is vertical shift and r is radius.

That means we have to complete the square for both x-term and y-term.

Rearrange the equation:

`\displaystyle \large{x^2-6x+y^2+2y+1=0}\\\displaystyle \large{(x^2-6x)+(y^2+2y+1)=0}`

For
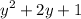`\displaystyle \large{y^2+2y+1}`, can be converted to perfect square as
`\displaystyle \large{(y+1)^2}`. Hence:

`\displaystyle \large{(x^2-6x)+(y+1)^2=0}`

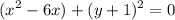
For the x-terms, we have to find another value that can complete the square. We know that
`\displaystyle \large{(a\pm b)^2 = a^2 \pm 2ab + b^2}`.

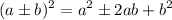For
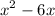`\displaystyle \large{x^2-6x}` can be
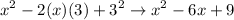`\displaystyle \large{x^2-2(x)(3)+3^2 \to x^2-6x+9}`. So our another value is 9.

`\displaystyle \large{(x^2-6x+9-9)+(y+1)^2=0}`

From above, we add -9 because the original expression isn’t actual perfect square.

Separate -9 out of
`\displaystyle \large{x^2-6x+9}`:

`\displaystyle \large{(x^2-6x+9)-9+(y+1)^2=0}`

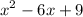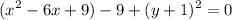
Transport -9 to add another side:

`\displaystyle \large{(x^2-6x+9)+(y+1)^2=9}`

Complete the square:

`\displaystyle \large{(x-3)^2+(y+1)^2=9}`

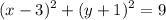
Finally, we have our needed equation to find radius and center. The coordinate of center is defined as the point (h,k) from
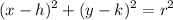`\displaystyle \large{(x-h)^2+(y-k)^2=r^2}` and the radius is defined as r.

Hence, from the equation:

The coordinate of center is (3,-1) with radius equal to 3.