Answer:
The population will reach 860,000 in 16.67 years from now.
Explanation:
The compound growth model is given by the following equation:
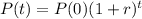
In which
 is the initial population and r is the growth rate(decimal).
is the initial population and r is the growth rate(decimal).
In this problem, we have that:
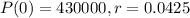
Approximately when will the population reach 860,000?
This is t when
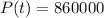 . So
. So
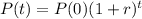
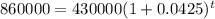
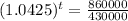
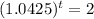
We have the following logarithm rule
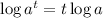
Applying log to both sides
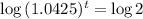
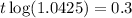

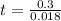
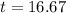
The population will reach 860,000 in 16.67 years from now.