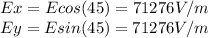Question

Four particles are located at the corners of a square that is 50 mm on a side. All four particles carry a charge of magnitude 7.0 nC , with positive charge at the lower left corner and negative charge at the other corners. Assume that the positive x and y axes are directed to the right and upward, respectively, and that the sides of the square are parallel to these coordinate axes.

Part A

Determine the x component of the electric field at the center of the square.

Part B

Determine the y component of the electric field at the center of the square.

Answer 1

Part A: 142552 V/m; Part B: 142552 V/m

Step-by-step explanation:

Electric field is a vector, directed from the positive charges and ending on the negative charges. The lines are straight.

For the given case, in the center of the square, all four charges create the following fields, if we look at each one individually:

Positive charge creates a field, which is directed upwards, with the 45-degree angle to the positive direction of the x-axis;

Negative charge, located on the top left corner, creates electric field, which is directed on the 135-degree angle with respect to x-axis;

Negative charge. located on the top right corner, creates an electric field, which is directed on the 45-degree angle with respect to the x-axis;

Negative charge, located on the bottom right corner, create an electric field, which is directed on the -45 degree angle with respect to x-axis.

As if can be seen, fields created by top-left and bottom-right negative charges have opposite directions, so the combined field from these two charges is zero (0 V/m), once the vector addition is performed.

On the other hand, fields from the positive charge and negative charge in the top right corner, have the same direction, thus the overall field will be combined by each field from these charges.

To calculate field, created by a charge, we can use the following equation:

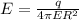`E=(q)/(4\pi E R^(2) )` where R- distance to the testing point, E- dielectric constant, q- charge value.

For the given conditions, the field is directed on the +45 degree angle with respect to the x-axis and its value can be determined by the following equation:

`E=Epos+Eneg=(q)/(4\pi E R^(2) )+ (q)/(4\pi E R^(2) )=100800 V/m`

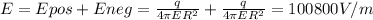
Note, that the distance between the charges and the testing point in the center of the square R:
`R=0.5*50*√(2)=35.36 mm`

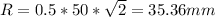
As far, as the field is directed upwards, both components for x- and y-axes will be positive and can be calculated, using cos and sin function, respectively.

`Ex=E cos (45)= 71276 V/m\\Ey= E sin (45) = 71276 V/m`