Question

In ΔBCD, the measure of ∠D=90°, the measure of ∠C=77°, and CD = 41 feet. Find the length of BC to the nearest foot.

I NEED HELP PLEASEEEEEEEEEEEEEEE

Answer 1

182 ft

Explanation:

When you are not given a diagram, always draw one for yourself (see diagram).

When you have a right triangle (triangle with 90° angle), you can use the trigonometry ratios, You can remember them using SohCahToa. It is read like this:

sinθ = opposite/hypotenuse Soh

cosθ = adjacent/hypotenuse Cah

tanθ = opposite/adjacent Toa

"θ" means the angle of reference (the angle you are talking about).

We are looking for the length of BC, which is the hypotenuse. I labelled it "d" (lowercase D) because it is opposite to ∠D.

We know ∠C = 77°. This will be our angle of reference (replace θ).

The side we know is DC, also known as "b" (lowercase B) because it's opposite to ∠B. "b" is the adjacent side when θ = C because "b" is touching ∠C.

Take the general trig. formula that has hypotenuse and adjacent: (cosine ratio)

cosθ = adjacent/hypotenuse

Substitute the variables specific for this problem.

cosC = b/d

Substitute the values you know.

cos77° = (41 ft) / d

Isolate "d" to the left side

dcos77° =
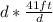`d*(41ft)/(d)` Multiply both sides by "d"

dcos77° = 41 ft

dcos77° / cos77° = 41 ft / cos77° Divide both sides by cos77°

d = 41 ft / cos77° Input into calculator

d = 182.261874....... ft Unrounded answer

d ≈ 182 ft Rounded to nearest foot (whole number)

Remember d = BC. It's often easier to use one letter for calculations.

Therefore the length of BC is about 182 feet.