The angle of elevation of the ground is 30.5°
Explanation:
Height of the tree=10 foot
length of the shadow=17 foot
we have to determine the angle of elevation of the ground
The tree, shadow and ground forms a right triangle with tree as the height, shadow as the base.
The angle of elevation of the ground θ
tanθ=opposite/adjacent
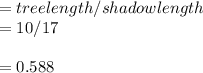
θ

The angle of elevation of the ground is 30.5°