Answer:
A) 11
Explanation:
Let M and A represent number of boxes of cookies sold by Mark and Ann respectively.
We have been given that Mark sold 10 boxes less than n. We can represent this information as:
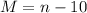 .
.
Ann sold 2 boxes less than n, so number of boxes of cookies sold by Ann would be
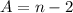 .
.
Further we are told that Mark and Ann have each sold at least one box of cookies, so we will get:
 and
and
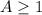 .
.
Now, we can set two inequality as:
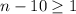 and
and

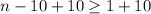 and
and
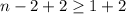
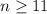 and
and
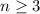
We are also told that together they have sold less than n boxes. We can represent this information in an inequality as:
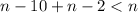
Let us solve for n.

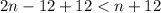
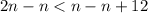
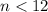
Upon combining our inequalities
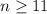 ,
,
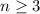 and
and
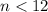 , we can see that the value of n that will be less than 12 and greater than or equal to 11 is 11.
, we can see that the value of n that will be less than 12 and greater than or equal to 11 is 11.
Therefore, the value of n is 11 and option A is correct choice.