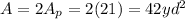Question

Helphelphelp helphelphelp helphelphelp helphelphelp helphelphelp​

Answer 1

3)
`55.2 in^2`

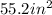
4)
`42 yd^2`

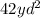
Explanation:

3)

The regular hexagon can be seen as consisting of 6 identical triangles, so its area is equal to six times the area of one triangle:

`A=6A_T`

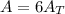
The area of one triangle can be written as:

`A_T=(1)/(2)bh`

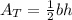
where:

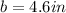`b=4.6 in` is the base of the triangle

`h=4 in` is the height

Substituting,

`A_T=(1)/(2)(4.6)(4)=9.2 in^2`

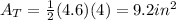
And so, the area of the regular hexagon is:

`A=6A_T=6(9.2)=55.2 in^2`

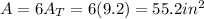
4)

Here we have a complex figure consisting of several regular figures.

We observe that the figure consists of 2 parallelograms, on top and on bottom, so the total area of the figure is the sum of the areas of the two parallelograms:

`A=2A_p`

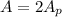
where
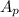`A_p` is the area of one parallelogram, which is given by

`A_p = bh`

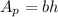
where:

b = 7 yd is the base of the parallelogram

h = 3 yd is the height of the parallelogram

Therefore, the area of the parallelogram is

`A_p=(7)(3)=21 yd^2`

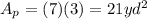
And therefore, the area of the figure is:

`A=2A_p=2(21)=42 yd^2`