Answer:
54.02m
Step-by-step explanation:
According to Newton's second law of motion;
∑F = m x a ------------------(i)
Where;
∑F = effective force acting on a body
m = mass of the body
a = acceleration of the body
(i) According to the question, the only force acting on the horizontal (direction of motion) is the frictional force (
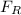 ) between the tires of the automobile and the dry pavement and it is directed opposite the direction of motion. Therefore, it is negative.
) between the tires of the automobile and the dry pavement and it is directed opposite the direction of motion. Therefore, it is negative.
i.e ∑F = -
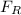
Where;
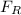 = μ
= μ
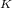 x N
x N
μ
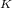 = coefficient of kinetic friction.
= coefficient of kinetic friction.
N = normal reaction = m x g
m = mass of the automobile as depicted by the tires and
g = acceleration due to gravity = 10m/s²
=> ∑F = - μ
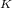 x m x g
x m x g
Substitute the value of ∑F into equation (i) as follows;
- μ
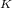 x m x g = m x a
x m x g = m x a
Divide through by m;
- μ
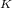 x g = a ------------------(ii)
x g = a ------------------(ii)
Given;
μ
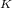 = Coefficient of kinetic friction between tires and dry = 0.800
= Coefficient of kinetic friction between tires and dry = 0.800
Substitute this value into equation (ii) as follows;
- 0.800 x 10 = a
a = - 8m/s²
Therefore, the acceleration of the automobile is -8m/s² [The negative sign shows deceleration]
(ii) Now, the distance (s) is gotten from one of the equations of motion as follows;
v² = u² + 2as ---------------------(iii)
Where
v = final velocity of the automobile = 0 [since the automobile is stopped]
u = initial velocity of the automobile = 29.4m/s
a = acceleration of the automobile = - 8m/s²
Substitute these values into equation (iii) as follows;
0² = 29.4² + [2(-8) x s]
0 = 864.36 - 16s
16s = 864.36
Solve for s;
s =
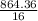
s = 54.02m
Therefore, the shortest distance in which the automobile can be stopped by locking the brakes when traveling at 29.4m/s is 54.02m