Question

Iridium has only two naturally occurring isotopes. Ir-191 with arelative mass of 190.96058 and Ir-193 with a relative mass of192.96292. Compute the fractional abundance of Ir-191.

Answer 1

Answer: The fractional abundance of Ir-191 is 0.372

Step-by-step explanation:

Average atomic mass of an element is defined as the sum of masses of each isotope each multiplied by their natural fractional abundance.

Formula used to calculate average atomic mass follows:

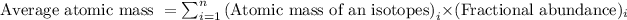`\text{Average atomic mass }=\sum_(i=1)^n\text{(Atomic mass of an isotopes)}_i* \text{(Fractional abundance})_i` .....(1)

Let the fractional abundance of Ir-191 be x and that of Ir-193 isotope be (1-x)

For isotope 1 (Ir-191):

Mass of isotope 1 = 190.96058 amu

Fractional abundance of Ir-191 = x

For isotope 1 (Ir-193):

Mass of isotope 1 = 192.96292 amu

Fractional abundance of Ir-193 = (1 - x)

Average atomic mass of iridium = 192.217 amu

Putting values in equation 1, we get:

`192.217=[(190.96058* x)+(192.96292* (1-x))]\\\\x=0.372`

Hence, the fractional abundance of Ir-191 is 0.372