Question

What is the vapor pressure of the solution if 35.0 g of water is dissolved in 100.0 g of ethyl alcohol at 25 ∘C? The vapor pressure of pure water is 23.8 mmHg, and the vapor pressure of ethyl alcohol is 61.2 mmHg at 25 ∘C.

Answer 1

Answer: The vapor pressure of the solution is 43.55 mmHg

Step-by-step explanation:

To calculate the number of moles, we use the equation:

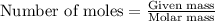`\text{Number of moles}=\frac{\text{Given mass}}{\text{Molar mass}}` .....(1)

• For water:

Given mass of water = 35.0 g

Molar mass of water = 18 g/mol

Putting values in equation 1, we get:

`\text{Moles of water}=(35.0g)/(18g/mol)=1.944mol`

• For ethyl alcohol:

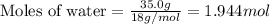
Given mass of ethyl alcohol = 100.0 g

Molar mass of ethyl alcohol = 46 g/mol

Putting values in equation 1, we get:

`\text{Moles of ethyl alcohol}=(100.0g)/(46g/mol)=2.174mol`

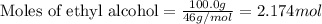
Total moles of solution = [1.944 = 2.174] moles = 4.118 moles

• Mole fraction of a substance is given by:

`\chi_A=(n_A)/(n_A+n_B)`

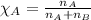
For water:

`\chi_{\text{water}}=\frac{n_{\text{water}}}{n_{\text{water}}+n_{\text{ethyl alcohol}}}`

`\chi_(water)=(1.944)/(4.118)=0.472`

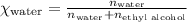
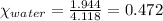
For ethyl alcohol:

`\chi_{\text{ethyl alcohol}}=\frac{n_{\text{ethyl alcohol}}}{n_{\text{water}}+n_{\text{ethyl alcohol}}}`

`\chi_{\text{ethyl alcohol}}=(2.174)/(4.118)=0.528`

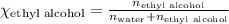
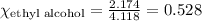
Dalton's law of partial pressure states that the total pressure of the system is equal to the sum of partial pressure of each component present in it.

To calculate the vapor pressure of the solution, we use the law given by Dalton, which is:

`P_T=\sum_(i=1)^n (p_i* \chi_i)`

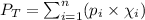
Or,

`P_T=[(p_{\text{water}}* \chi_{\text{water}})+(p_{\text{ethyl alcohol}}* \chi_{\text{ethyl alcohol}}`

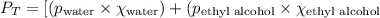
We are given:

Vapor pressure of water = 23.8 mmHg

Vapor pressure of ethyl alcohol = 61.2 mmHg

Putting values in above equation, we get:

`p_T=[(23.8* 0.472)+(61.2* 0.528)]\\\\p_T=43.55mmHg`

Hence, the vapor pressure of the solution is 43.55 mmHg