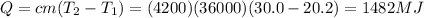Question

A swimming pool, 10.0 m by 4.0 m is filled to a depth of 3.0 m with water at a temperature of 20.2oC. How much energy is required to raise the temperature of the water to 30.0 oC?

Answer 1

It is required 1482 Megajoules of energy.

Step-by-step explanation:

The energy Q required to raise the temperature T1 to a temperature T2 of mass m of water is:

`Q=cm\(T_2-T_1)` (1)

with c the specific heat of water that is
`c=4200(J)/(kg oC)`.

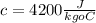We don't have explicit the mass of water containded in the swimming pool, but we can use the relation:

`m=V\rho`

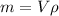
with ρ the density of water that is
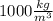`1000(kg)/(m^3)`, V the volume of the swimming pool and m the mass, so m is:

`m=(3.0)(4.0)(3.0)1000=36000kg`

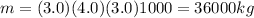
Using c and m on (1):

`Q=cm(T_2-T_1)=(4200)(36000)(30.0-20.2)=1482 MJ`