Answer:
19.34°C
Step-by-step explanation:
When the ice cube is placed in the water, heat will be transferred from the hot water to it such that the heat gained (Q₁) by the ice is equal to the heat lost(Q₂) by the hot water and a final equilibrium temperature is reached between the melted ice and the cooling/cooled hot water. i.e
Q₁ = -Q₂ ----------------------(i)
{A} Q₁ is the heat gained by the ice and it is given by the sum of ;
(i) the heat required to raise the temperature of the ice from -30°C to 0°C. This is given by [m₁ x c₁ x ΔT]
Where;
m₁ = mass of ice = 0.0550kg
c₁ = a constant called specific heat capacity of ice = 2108J/kg°C
ΔT₁ = change in the temperature of ice as it melts from -30°C to 0°C = [0 - (-30)]°C = [0 + 30]°C = 30°C
(ii) and the heat required to melt the ice completely - This is called the heat of fusion. This is given by [m₁ x L₁]
Where;
m₁ = mass of ice = 0.0550kg
L₁ = a constant called latent heat of fusion of ice = 334 x 10³J/kg
Therefore,
Q₁ = [m₁ x c₁ x ΔT₁] + [m₁ x L₁] ------------------(ii)
Substitute the values of m₁, c₁, ΔT₁ and L₁ into equation (ii) as follows;
Q₁ = [0.0550 x 2108 x 30] + [0.0550 x 334 x 10³]
Q₁ = [3478.2] + [18370]
Q₁ = 21848.2 J
{B} Q₂ is the heat lost by the hot water and is given by
Q₂ = m₂ x c₂ x ΔT₂ -----------------(iii)
Where;
m₂ = mass of water = 0.400kg
c₂ = a constant called specific heat capacity of water = 4200J/Kg°C
ΔT₂ = change in the temperature of water as it cools from 35°C to the final temperature of the hot water (T) = (T - 35)°C
Substitute these values into equation (iii) as follows;
Q₂ = 0.400 x 4200 x (T - 35)
Q₂ = 1680 x (T-35) J
{C} Now to get the final temperature, substitute the values of Q₁ and Q₂ into equation (i) as follows;
Q₁ = -Q₂
=> 21848.2 = - 1680 x (T-35)
=> 35 - T = 21848.2 / 1680
=> 35 - T = 13
=> T = 35 - 13
=> T = 22
Therefore the final temperature of the hot water is 22°C.
Now let's find the final temperature of the mixture.
The mixture contains hot water at 22°C and melted ice at 0°C
At this temperature, the heat (
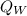 ) due to the hot water will be equal to the negative of the one (
) due to the hot water will be equal to the negative of the one (
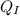 ) due to the melted ice.
) due to the melted ice.
i.e
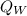 = -
= -
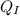 -----------------(a)
-----------------(a)
Where;
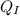 =
=
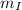 x
x
 x Δ
x Δ
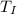 [
[
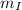 = mass of ice,
= mass of ice,
 = specific heat capacity of melted ice which is now water and Δ
= specific heat capacity of melted ice which is now water and Δ
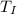 = change in temperature of the melted ice]
= change in temperature of the melted ice]
and
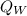 =
=
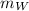 x
x
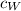 x Δ
x Δ

[
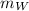 = mass of water,
= mass of water,
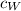 = specific heat capacity of water and Δ
= specific heat capacity of water and Δ
 = change in temperature of the water]
= change in temperature of the water]
Substitute the values of
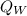 and
and
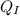 into equation (a) as follows
into equation (a) as follows
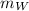 x
x
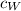 x Δ
x Δ
 = -
= -
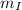 x
x
 x Δ
x Δ
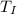
Note that
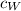 and
and
 are the same since they are both specific heat capacities of water. Therefore, the equation above becomes;
are the same since they are both specific heat capacities of water. Therefore, the equation above becomes;
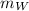 x Δ
x Δ
 = -
= -
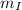 x Δ
x Δ
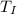 -----------------------(b)
-----------------------(b)
Now, let's analyse Δ
 and Δ
and Δ
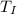 . The final temperature (
. The final temperature (
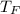 ) of the two kinds of water(melted ice and cooled water) are now the same.
) of the two kinds of water(melted ice and cooled water) are now the same.
=> Δ
 = change in temperature of water = final temperature of water(
= change in temperature of water = final temperature of water(
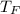 ) - initial temperature of water(
) - initial temperature of water(
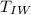 )
)
Δ
 =
=
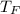 -
-
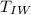
Where;
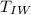 = 22°C [which is the final temperature of water before mixture]
= 22°C [which is the final temperature of water before mixture]
=> Δ
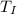 = change in temperature of melted ice = final temperature of water(
= change in temperature of melted ice = final temperature of water(
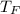 ) - initial temperature of melted ice (
) - initial temperature of melted ice (
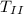 )
)
Δ
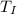 =
=
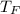 -
-
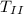
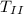 = 0°C (Initial temperature of the melted ice)
= 0°C (Initial temperature of the melted ice)
Substitute these values into equation (b) as follows;
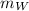 x Δ
x Δ
 = -
= -
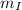 x Δ
x Δ
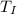
0.400 x (
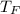 -
-
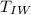 ) = -0.0550 x (
) = -0.0550 x (
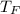 -
-
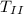 )
)
0.400 x (
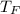 - 22) = -0.0550 x (
- 22) = -0.0550 x (
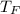 - 0)
- 0)
0.400 x (
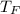 - 22) = -0.0550 x (
- 22) = -0.0550 x (
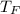 )
)
0.400
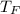 - 8.8 = -0.0550
- 8.8 = -0.0550
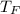
0.400
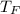 + 0.0550
+ 0.0550
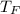 = 8.8
= 8.8
0.455
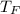 = 8.8
= 8.8
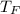 = 19.34°C
= 19.34°C
Therefore, the final temperature of the mixture is 19.34°C