Answer:
C =

Explanation:
given A varies directly as B and inversely as C then the equation relating them is
A =
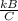 ← k is the constant of variation
← k is the constant of variation
to find k use the condition A = 6 , B = 10 , C = 15 , then
6 =
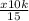 ( multiply both sides by 15 )
( multiply both sides by 15 )
90 = 10k ( divide both sides by 10 )
9 = k
A =
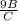 ← equation of variation
← equation of variation
when A = 92 and B = 107 , then
92 =
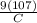 ( multiply both sides by C )
( multiply both sides by C )
92C = 963 ( divide both sides by 92 )
C =
