Question

Of 200 youthful gamers (under 18) who tried the new Z-Box-Plus game, 160 rated it "excellent," compared with only 144 of 200 adult gamers (18 or over). The test statistic to test if the two proportions differed significantly would be a. 1645 b. 1.960 c. 1.873 d. 1448

Answer 1

Correct option is (c). 1.873.

Explanation:

The hypothesis can be defined as:

H₀: There is no difference between the two proportions.

Hₐ: There is a difference between the two proportions.

Given:

`X_(1) = 160,\ n_(1)=200\\X_(2) = 144,\ n_(2)=200`

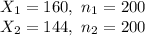
The sample proportion of youthful gamers who tried the new Z-Box-Plus game and rated it "excellent," is:

`\hat p_(1)=(X_(1))/(n_(1)) =(160)/(200) =0.80`

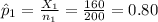
The sample proportion of adult gamers who tried the new Z-Box-Plus game and rated it "excellent," is:

`\hat p_(2)=(X_(2))/(n_(2)) =(144)/(200) =0.72`

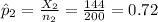
The population proportion of gamers who rated the game as "excellent" is:

`P=(X_(1)+X_(2))/(n_(1)+n_(2)) =(160+144)/(200+200)= 0.76`

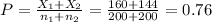
The test statistic is:

`z=\frac{\hat p_(1)-\hat p_(2)}{\sqrt{P(1-P)[(1)/(n_(1))+(1)/(n_(2)) ]} } =\frac{0.80-0.72}{\sqrt{0.76(1-0.76)[(1)/(200)+(1)/(200) ]} }=1.873`

Thus, the value of the test statistic is 1.873.

The correct option is (c).