Question

Raindrops fall 1700 m from a cloud to the ground. (a) If they were not slowed by air resistance, how fast would the drops be moving when they struck the ground? (b) Would it be safe to walk outside during a rainstorm?

Answer 1

a) 182.54m/s

b) In that case it would not be safe to walk outside during a rainstorm.

Step-by-step explanation:

We use the third equation of motion of free fall under gravity to determine the velocity with which the raindrops will strike the ground.

`v^2=u^2+2gh.................(1)`

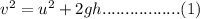
were v is the velocity with which they strike the ground, g is acceleration due to gravity taken as
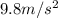`9.8m/s^2`, h is the height from which the drops fall.

Given;

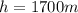`h=1700m\\`, u = 0m/s since the raindrops are assumed to drop freely from rest.

Therefore;

`v^2=0^2+2*9.8*1700\\v^2=33320\\v=√(33320)\\ v=182.54m/s`

At this velocity I think it will not be safe to walk outside during a rainstorm because millions of water molecules falling at this speed will cumulatively posses a very high amount of kinetic energy that will impact whoever comes under it. The water molecules may also appear as a fast flowing river.

It is only if the mass of water molecules is completely neglected that it might still be safe to walk under a rainstorm in such case.