Question

On Dolphin Beach, the high tide is 1.8 meters and only occurs at 12 a.m. and 12 p.m. The low tide is 0.4 meter and only occurs at 6 a.m. and 6 p.m.

Which function models the height of the tide t hours after 12 a.m.?




h(t)=0.7cos(πt/6)+1.1

h(t)=1.8cos(πt/3)+0.4

h(t)=1.1sin(πt/3)+0.7

h(t)=0.7sin(πt/6)+1.1

Answer 1

h(t)=0.7sin(πt/6)+1.1

Explanation:

A periodic function that models the height of the tide can be written as

`h(t)=A cos(\omega t)+y_c`

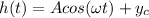
where

A is the amplitude

`\omega` is the angular frequency

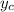`y_c` is the central value of the tide

Here we know that:

- the hight tide is 1.8 meters

- the low tide is 0.4 meters

So, the central value of the tide is

`y_c = (1.8+0.4)/(2)=1.1 m`

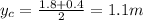
Also, the amplitude is the maximum displacement from the equilibrium position (central value of the tide), so:

`A=1.8-y_c = 1.8-1.1 = 0.7 m`

Now we have to find the angular frequency, which is related to the period T by

`\omega=(2\pi)/(T)`

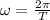
Here the high tide occurs at 12 am and 12 pm: this means that the period is 12 hours, so

T = 12

`\omega=(2\pi)/(12)=(\pi)/(6)`

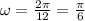
Therefore, the correct equation is

h(t)=0.7sin(πt/6)+1.1