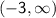Question

Find the domain over which the function y = x + 6x is monotonic increasing.

Answer 1

x > -3

`\sf (-3, \infty)`

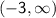
Explanation:

Domain: input values (x-values)

Monotonic increasing: always increasing.
A function is increasing when its graph rises from left to right.

The graph of a quadratic function is a parabola. If the leading term is positive, the parabola opens upwards. The domain over which the function is increasing for a parabola that opens upwards is values greater than the x-value of the vertex.

Vertex

Standard form of quadratic equation:
`\sf y=ax^2+bx+c`

`\textsf{x-value of vertex}=\sf -(b)/(2a)`

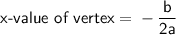
Given function:

`\sf y=x^2+6x`

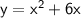
Therefore, x-value of function's vertex:

`\sf \implies x= -(6)/(2)=-3`

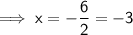
Final Solution

The function is increasing when x > -3

`\sf (-3, \infty)`