Question

For the cost function, find the marginal cost at the given production level x. State the units of measurement. (All costs are in dollars.) HINT [See Example 1.] C(x) = 15,000 + 50x + 1,000 x ; x = 100

Answer 1

The marginal cost at the given production level is $49.9.

Explanation:

The marginal cost function is expressed as the first derivative of the total cost function with respect to quantity (x).

We have that the cost function is given by

`C(x) = 15000 + 50x + (1000)/(x)`

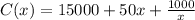
So, we need the derivative and then we’ll need to compute the value x = 100 of the derivative.

`C'(x)=(d)/(dx)\left(15000+50x+(1000)/(x)\right)\\\\\mathrm{Apply\:the\:Sum/Difference\:Rule}:\quad \left(f\pm g\right)'=f\:'\pm g'\\\\C'(x)=(d)/(dx)\left(15000\right)+(d)/(dx)\left(50x\right)+(d)/(dx)\left((1000)/(x)\right)\\\\C'(x)=0+50-(1000)/(x^2)\\\\C'(x)=50-(1000)/(x^2)`

When x = 100, the marginal cost is

`C'(100)=-(1000)/(100^2)+50\\\\C'(100)=(499)/(10)=49.9`