Question

Find an equation of combined variation where a varies directly as b and inversely as c. One set of values is a = 4, b = 12, and c = 9. Find a when b = 7 and c = 3.

Answer 1

Combined equation is
`a = (kb)/(c)`

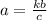
Explanation:

a varies directly as b and inversely as c.

This can be written as

a =
`k * b`

a = kb

where k is the proportionality constant

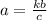`a = (kb)/(c)`-------------------------------------(1)

Now lets find the k value bu substituting the given a, b,c values

`4 = (k (12))/(9)`

`9 * 4 = 12k`

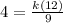
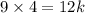
36 = 12 k

`k = (36)/(12)`

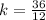
k = 3

Thus the eq(1) becomes

`a = (3b)/(c)`

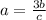
Let us now find the value of a when b=7 and c = 3

`a = (3(7))/(3)`

`a =(21)/(7)`

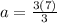
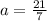
a = 7