Question

With a ruler, Diamond determines the diameter of a golf ball to be 4.2 centimeters (a radius of 2.1 cm) and the diameter of a practice softball to be 8.4 centimeters (a radius of 4.2 cm). Diamond erroneously claims that the softball has twice the volume of the golf ball. In a short paragraph, explain Diamonds misconceptions. Use the formula for the volume of a sphere to determine the volume of both the golf ball and the softball in cubic centimeters and then compare their volumes. (Hint: Golf Ball Volume V = 4/3 π r3 ; V = 4/3 ∙ (3.14) ∙ (2.1)3 ) (Hint: Softball Volume V = 4/3 π r3 ; V = 4/3 ∙ (3.14) ∙ (4.2)3 )

Answer 1

Diamonds is incorrect, because, the volume of the softball is 8 times the volume of the golf ball

Explanation:

we know that

The volume of a sphere is equal to

`V=(4)/(3)\pi r^(3)`

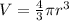
where

r is the radius

step 1

Find the volume of the golf ball

we have

`r=2.1\ cm\\pi =3.14`

substitute

`V=(4)/(3)(3.14)(2.1)^(3)=38.77\ cm^3`

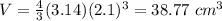
step 2

Find the volume of the the softball

we have

`r=4.2\ cm\\pi =3.14`

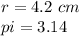
substitute

`V=(4)/(3)(3.14)(4.2)^(3)=310.18\ cm^3`

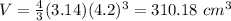
step 3

Find the ratio of volumes

Divide the volume of the softball by the volume of the golf ball

`(310.18)/(38.77)=8`

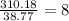
That means

Diamonds is incorrect, because, the volume of the softball is 8 times the volume of the golf ball