Answer:
For maximum surface area the width of the pool is 22 feet and length of the pool be 22 feet.
Explanation:
Here the Perimeter of the rectangular pool is 88 feet.
Let us suppose that the length of the pool be a feet and width of the pool be b feet.
Therefore the perimeter of the pool is = 2(a+b)
Therefore, according to the condition,
2(a+b) = 88
or, a+b = 44
or, a= 44 - b
Now the area of the pool is = ab = (44-b)b (since, a= 44 - b)
Let us suppose y = (44-b)b
or,y =
 .
.
We have to find the maximum value of the surface area y.
Now, differentiating y with respect b, we get
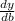 = 44 - 2b
= 44 - 2b
Again, differentiating
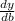 with respect b, we get
with respect b, we get
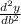 = -2 , which is always less than zero for any value of b.
= -2 , which is always less than zero for any value of b.
therefore, y has maximum value at 44 - 2b = 0
or, b= 22.
Therefore for maximum surface area the width of the pool is 22 feet and length of the pool be (44-22) =22 feet.