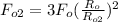Question

The electric force between two charged objects of charge +Q0 that are separated by a distance R0 is F0. The charge of one of the objects is increased to +3Q0, and the separation distance between the objects is reduced to R02. In terms of F0, what is the new electric force between the two objects?

Answer 1

`F=3F_o((R_o)/(R_(o2)))^2`

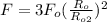
Step-by-step explanation:

This problem is approached using Coulomb's law of electrostatic attraction which states that the force F of attraction or repulsion between two point charges,
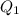`Q_1` and
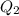`Q_2` is directly proportional to the product of the charges and inversely proportional to the square of their distance of separation R.

`F=(kQ_1Q_2)/(R^2)..................(1)`

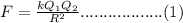
where k is the electrostatic constant.

We can make k the subject of formula as follows;

`k=(FR^2)/(Q_1Q_2)...........(2)`

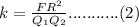
Since k is a constant, equation (2) implies that the ratio of the product of the of the force and the distance between two charges to the product of charges is a constant. Hence if we alter the charges or their distance of separation and take the same ratio as stated in equation(2) we will get the same result, which is k.

According to the problem, one of the two identical charges was altered from
`Q_o` to
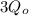`3Q_o` and their distance of separation from
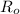`R_o` to
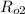`R_(o2)`, this also made the force between them to change from
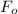`F_o` to
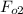`F_(o2)`. Therefore as stated by equation (2), we can write the following;

`(F_oR_o^2)/(Q_o*Q_o)=(F_(o2)R_(o2)^2)/(3Q_o*Q_o).............(3)`

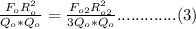
Therefore;

`(F_oR_o^2)/(Q_o^2)=(F_(o2)R_(o2)^2)/(3Q_o^2).............(4)`

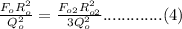
From equation (4) we now make the new force
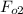`F_(o2)` the subject of formula as follows;

`{F_oR_o^2}*{3Q_o^2}=F_(o2)R_(o2)^2*{Q_o^2}`

`Q_o` then cancels out from both side of the equation, hence we obtain the following;

`3{F_oR_o^2}=F_(o2)R_(o2)^2.............(4)`

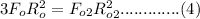
From equation (4) we can now write the following;

`F_(o2)=(3F_oR_o^2)/(R_(o2)^2)`

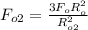
This could also be expressed as follows;

`F_(o2)=3F_o((R_o)/(R_(o2)))^2`