Question

The volume V of a right‑circular cylinder is computed using the values d = 3.1 m for the diameter and h = 6.6 m for the height. Use the Linear Approximation to estimate the maximum error R in V if each of these values has a possible error of at most 2 % . Recall that V = π r 2 h .

Answer 1

6%

Explanation:

A function f(x) can by approximated at and around a point, say x = a by,

f(x) = f(a) + f'(a)(x-a)

where,
`f'(x)=(df)/(dx)`

Here, volume V is a function of radius r and height h. In the 2 dimensional case, we have to take the partial derivatives.

Given,

`V=\pi r^2h`

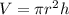
or,
`dV=(\partial V )/(\partial r)dr+ (\partial V )/(\partial h)dh`

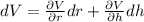
at r = 1.55 m and h = 6.6 m

`dr=0.02*1.55m=0.031m`

`dh=0.02*6.6m=0.132m`

`(\partial V )/(\partial r)=2\pi r h=2\pi * 1.55* 6.6=64.277`

`(\partial V )/(\partial h)=\pi r^2=7.5477`

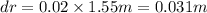
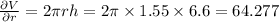
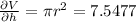
Therefore,
`dV=(64.277*.031)+(7.5477*0.132)=2.9889m`

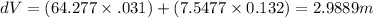
Also,
`V=\pi r^2h=49.8147m`

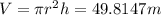
Hence, maximum error is given by,

`R=(2.9889)/(49.8147) * 100`

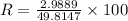
= 6%