2 Answers

StuffandBlah · Answer 1 · 2021-07-27T04:15:57+0000

Option D:
$x\sqrt[9]{y^2}$ is the expression equivalent to
$xy^{(2)/(9)}$

Step-by-step explanation:

Option A:
√(xy^9)

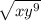
The expression can be written as
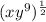
$({xy^9})^{(1)/(2)$

Applying exponent rule, we get,

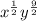
$x^{(1)/(2)} y^{(9)/(2)}$

Thus, the expression
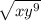√(xy^9) is not equivalent to the expression
$xy^{(2)/(9)}$

Hence, Option A is not the correct answer.

Option B:
$\sqrt[9]{xy^2}$

The expression can be written as
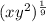
$({xy^2})^{(1)/(9)$

Applying exponent rule, we get,

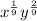
$x^{(1)/(9)} y^{(2)/(9)}$

Thus, the expression
$\sqrt[9]{xy^2}$ is not equivalent to the expression
$xy^{(2)/(9)}$

Hence, Option B is not the correct answer.

Option C:
x√(y^9)

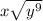
The expression can be written as
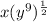
$x(y^9)^{(1)/(2) }$

Applying exponent rule, we get,

$x y^{(9)/(2)}$

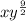
Thus, the expression
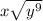x√(y^9) is not equivalent to the expression
$xy^{(2)/(9)}$

Hence, Option C is not the correct answer.

Option D:
$x\sqrt[9]{y^(2) }$

The expression can be written as
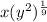
$x(y^2)^{(1)/(9) }$

Applying exponent rule, we get,

$xy^{(2)/(9)}$

Thus, the expression
$xy^{(2)/(9)}$ is equivalent to the expression
$xy^{(2)/(9)}$

Hence, Option D is the correct answer.

Please log in or register to add a comment.