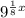Answer:
Explanation:
We want to find an equivalent expression for
![(\sqrt[4]{9})^{ (1)/(2)x}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/xdqwm8jhs06qn2xo2y8p7dlgd7ahdw6zgj.png)
To find an equivalent expression, we need to apply the following property of exponents:
![{a}^{ (m)/(n)}=( \sqrt[n]{ {a}} )^(m)](https://img.qammunity.org/2021/formulas/mathematics/middle-school/wy3x5ifxrz1bbk0qvd6ywshuw6zewpoqkd.png)
We let a=9, n=4 and m=½x
Then :
![{9}^{ ( (1)/(2)x)/(4)}=( \sqrt[4]{ {9}} )^{ (1)/(2)x}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/v1b67ttqp6pty0h06xm88ypfh37rf2jf5b.png)
Simplify the left hand side to get:
![{9}^ {(1)/(8)x} =( \sqrt[4]{ {9}} )^{ (1)/(2)x}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/jk8bi3gvuzckhjeem2sk8xj8vouudproot.png)
Therefore the correct answer is: