Question

You are driving down the road at 15 m/s you step on the gas and speed up with uniform acceleration of 2.5 m/s^2 for 0.80 seconds. If your tires have a radius of 34 cm, what is their angular displacement during this period of acceleration?

Answer 1

`x_f = 15 m/s *0.8 s + (1)/(2) 2.5 m/s^2 (0.8 s)^2 = 12.8 m`

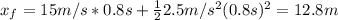
And we have the following relation between the angular displacement and the linear displacement:

`x = r \theta`

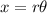
Where x represent the linear displacement and
`\theta` the angular displacement, if we solve for
`\theta` we got:

`\theta= (x)/(R)= (12.8 m)/(0.34 m)=37.65 rad`

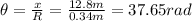
Step-by-step explanation:

For this case we have the following data given:

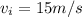`v_i = 15 m/s` represent the initial speed

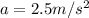`a = 2.5 m/s^2` represent the acceleration

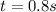`t = 0.8 s` represent the time

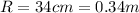`R = 34 cm = 0.34 m` represent the radius

First we can calculate the linear displacement with the following formula from kinematics:

`x_f = x_i + v_i t + (1)/(2) at^2`

And replacing we have:

`x_f = 15 m/s *0.8 s + (1)/(2) 2.5 m/s^2 (0.8 s)^2 = 12.8 m`

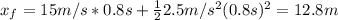
And we have the following relation between the angular displacement and the linear displacement:

`x = r \theta`

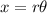
Where x represent the linear displacement and
`\theta` the angular displacement, if we solve for
`\theta` we got:

`\theta= (x)/(R)= (12.8 m)/(0.34 m)=37.65 rad`

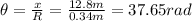
And that would be the angular displacement during the period of acceleration.