the answer will be option B 6.7
Step-by-step explanation: in co-ordinate geometry, let the P(x1, y1) and Q(x2, y2) be two points.
so their distance will be = sqaure root of ((x1 - x2)^2+(y1 - y2)^2)
here we take x1 = 1 , y1 = 2
and x2 = 4 , y2 = 8
so putting the values in the equation we get,

=
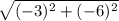
=
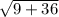
=
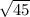
=6.70820393