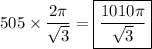Question

`\displaystyle \rm\int_(0)^( \infty ) \left( \frac{ {x}^(2) + 1}{ {x}^(4) + {x}^(2) + 1} \right) \left( \frac{ ln \left(1 - x + {x}^(2) - {x}^3 + \dots + {x}^(2020) \right) }{ ln(x) } \right) \: dx`​

Answer 1

Recall the geometric sum,

`\displaystyle \sum_(k=0)^(n-1) x^k = (1-x^k)/(1-x)`

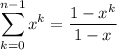
It follows that

`1 - x + x^2 - x^3 + \cdots + x^(2020) = (1 + x^(2021))/(1 + x)`

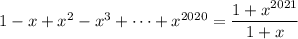
So, we can rewrite the integral as

`\displaystyle \int_0^\infty (x^2 + 1)/(x^4 + x^2 + 1) (\ln(1 + x^(2021)) - \ln(1 + x))/(\ln(x)) \, dx`

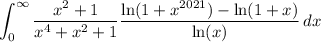
Split up the integral at x = 1, and consider the latter integral,

`\displaystyle \int_1^\infty (x^2 + 1)/(x^4 + x^2 + 1) (\ln(1 + x^(2021)) - \ln(1 + x))/(\ln(x)) \, dx`

Substitute
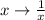`x\to\frac1x` to get

`\displaystyle \int_0^1 \frac{\frac1{x^2} + 1}{\frac1{x^4} + \frac1{x^2} + 1} \frac{\ln\left(1 + \frac1{x^(2021)}\right) - \ln\left(1 + \frac1x\right)}{\ln\left(\frac1x\right)} \, (dx)/(x^2)`

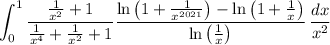
Rewrite the logarithms to expand the integral as

`\displaystyle - \int_0^1 (1+x^2)/(1+x^2+x^4) (\ln(x^(2021)+1) - \ln(x^(2021)) - \ln(x+1) + \ln(x))/(\ln(x)) \, dx`

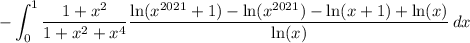
Grouping together terms in the numerator, we can write

`\displaystyle -\int_0^1 (1+x^2)/(1+x^2+x^4) (\ln(x^(2020)+1)-\ln(x+1))/(\ln(x)) \, dx + 2020 \int_0^1 (1+x^2)/(1+x^2+x^4) \, dx`

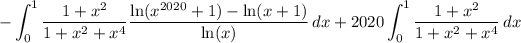
and the first term here will vanish with the other integral from the earlier split. So the original integral reduces to

`\displaystyle \int_0^\infty (1+x^2)/(1+x^2+x^4) (\ln(1-x+\cdots+x^(2020)))/(\ln(x)) \, dx = 2020 \int_0^1 (1+x^2)/(1+x^2+x^4) \, dx`

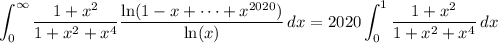
Substituting
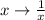`x\to\frac1x` again shows this integral is the same over (0, 1) as it is over (1, ∞), and since the integrand is even, we ultimately have

`\displaystyle \int_0^\infty (1+x^2)/(1+x^2+x^4) (\ln(1-x+\cdots+x^(2020)))/(\ln(x)) \, dx = 2020 \int_0^1 (1+x^2)/(1+x^2+x^4) \, dx \\\\ = 1010 \int_0^\infty (1+x^2)/(1+x^2+x^4) \, dx \\\\ = 505 \int_(-\infty)^\infty (1+x^2)/(1+x^2+x^4) \, dx`

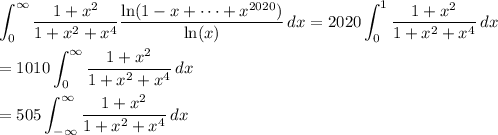
We can neatly handle the remaining integral with complex residues. Consider the contour integral

`\displaystyle \int_\gamma (1+z^2)/(1+z^2+z^4) \, dz`

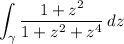
where γ is a semicircle with radius R centered at the origin, such that Im(z) ≥ 0, and the diameter corresponds to the interval [-R, R]. It's easy to show the integral over the semicircular arc vanishes as R → ∞. By the residue theorem,

`\displaystyle \int_(-\infty)^\infty (1+x^2)/(1+x^2+x^4)\, dx = 2\pi i \sum_\zeta \mathrm{Res}\left((1+z^2)/(1+z^2+z^4), z=\zeta\right)`

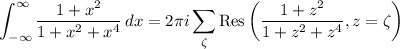
where
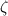`\zeta` denotes the roots of
`1+z^2+z^4` that lie in the interior of γ; these are
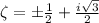`\zeta=\pm\frac12+\frac{i\sqrt3}2`. Compute the residues there, and we find

`\displaystyle \int_(-\infty)^\infty (1+x^2)/(1+x^2+x^4) \, dx = (2\pi)/(\sqrt3)`

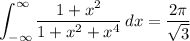
and so the original integral's value is

`505 * (2\pi)/(\sqrt3) = \boxed{(1010\pi)/(\sqrt3)}`