Answer:
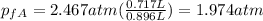


Step-by-step explanation:
For this case we can use the Boyle law given by:
Gas A
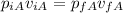
The final volume for this case would be the addition of the two volumes given
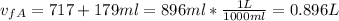
We can calculate the final pressure of the gas A:
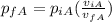
We need to remember that 1 bar = 1.01325 atm, we convert the initial pressure for the gas A and we got:
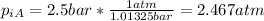
And finally we got:
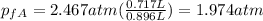
Gas B

The final volume for this case would be the addition of the two volumes given
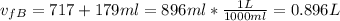
We can calculate the final pressure of the gas A:
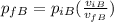
We need to remember that 1 bar = 1.01325 atm, we convert the initial pressure for the gas A and we got:
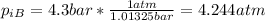
And finally we got:

And the total pressure for this case at the end would be:
