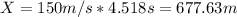Answer:
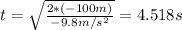
And now we can find the final distance on the x axis using the formula:
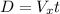
The velocity on x not changes and is the same plane spped
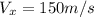 , if we replace we got:
, if we replace we got:
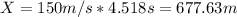
Step-by-step explanation:
For this case we have a illustration for the problem in the figure attached.
We need to find how far short of the target should be the plane, we have the following info given:
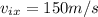
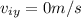
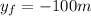
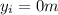
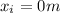
How far short of the target should it drop the package?
First we can find the total time in order to reach the groung using the following kinematic formula:
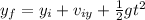
And replacing we have:
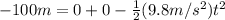
And solving for t we got:
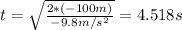
And now we can find the final distance on the x axis using the formula:
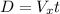
The velocity on x not changes and is the same plane spped
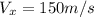 , if we replace we got:
, if we replace we got: