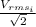Question

A sample of an ideal gas is slowly compressed to one-half its original volume with no change in pressure. If the original root-mean-square speed (thermal speed) of the gas molecules was V, the new speed is _____.(A) V/2.(B) V.(C) V/2(D)–√ 2V.(E) 2–√V.

Answer 1

`V_(rms_f)=\sqrt{(3PV)/(2nM)} = \sqrt{(1)/(2)} \sqrt{(3PV)/(M)} = (1)/(√(2)) \sqrt{(3PV)/(M)} = (1)/(√(2)) V_(rms_i)`

So then the final answer on this case would be:

`(V_(rms_i))/(√(2))`

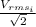
Step-by-step explanation:

From the kinetic theory model of gases we know that the velocity rms (speed of gas molecules) is given by:

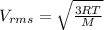`V_(rms)= \sqrt{(3RT)/(M)}` (1)

Where V represent the velocity

R the constant for ideal gases

T the temperature

M the molecular weight of the gas

We also know from the ideal gas law that
`PV= nRT`

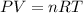
If we solve for T we got:
`T = (PV)/(nR)`

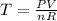
For the initial state we can replace T into the equation (1) and we got:

`V_(rms_i)= \sqrt{(3R ((PV)/(nR)))/(M)} = \sqrt{(3PV)/(M)}`

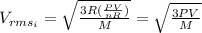
For the final state we know that :
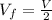`V_f = (V)/(2)` And the pressure not change , so then the final velocity would be:

`V_(rms_f)= \sqrt{(3R ((P(V/2))/(nR)))/(M)} = \sqrt{(3P(V/2))/(M)}`

`V_(rms_f)=\sqrt{(3PV)/(2nM)} = \sqrt{(1)/(2)} \sqrt{(3PV)/(M)} = (1)/(√(2)) \sqrt{(3PV)/(M)} = (1)/(√(2)) V_(rms_i)`

So then the final answer on this case would be:

`(V_(rms_i))/(√(2))`