Answer:
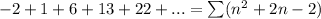
Explanation:
Series in Summation Notation
We must try to find a general formula for each term and then use summation to generalize the sum of all the terms for any value of n, the term number.
The series is
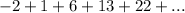
The difference between consecutive terms will be computed:

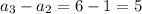

We can see that
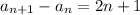
Applying summation on both sides:
![\sum [a_(n+1)-a_n]=\sum (2n+1)=\sum 2n+\sum 1](https://img.qammunity.org/2021/formulas/mathematics/college/1p4f0bj69qyc3ar42r3vnbyoh2dfrf0er4.png)
Knowing that
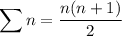
![\sum [a_(n+1)-a_n]=n(n+1)+n=n^2+2n](https://img.qammunity.org/2021/formulas/mathematics/college/y15yc7kv1b11tth2eodgrchuo70gb2oauo.png)
Similarly, the sum of the left side is found to be
![\sum [a_(n+1)-a_n]=a_(n+1)-a_1](https://img.qammunity.org/2021/formulas/mathematics/college/9x04dt7quxajejc1i8goiio6kp31923hyb.png)
Replacing into the above equation, we find
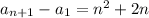
Solving
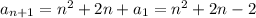
Having the general term, the series is expressed as
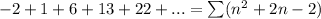
For n=0 to infinity