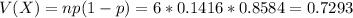Question

You’ve bought a half-dozen (six) eggs from the store but you forgot to check them first! The probability that no eggs are broken is 0.4. Otherwise, any number of broken eggs is equally probable. Define the random variable X = the number of broken eggs.

(a) Write out the pmf of X.
(b) Compute the probability that an even number of eggs is broken.

(c) Compute the expectation and variance of X.

Answer 1

a)

`P(X = 0) = C_(6,0).(0.1416)^(0).(0.8584)^(6) = 0.4`

`P(X = 1) = C_(6,1).(0.1416)^(1).(8584)^(5) = 0.3960`

`P(X = 2) = C_(6,2).(0.1416)^(2).(8584)^(4) = 0.1633`

`P(X = 3) = C_(6,3).(0.1416)^(3).(8584)^(3) = 0.0359`

`P(X = 4) = C_(6,4).(0.1416)^(4).(8584)^(2) = 0.0044`

`P(X = 5) = C_(6,5).(0.1416)^(5).(8584)^(1) = 0.0003`

`P(X = 6) = C_(6,6).(0.1416)^(6).(8584)^(0) = 0.00001`

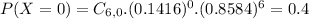
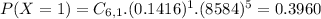
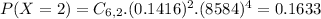
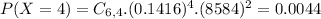
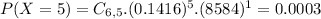
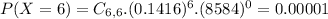
b) 56.77% probability that an even number of eggs is broken.

c)

Expectation: 0.8496

Variance: 0.7293

Explanation:

For each egg, there are only two possible outcomes. Either it is broken, or it is not. The probability of an egg being broken is independent from other eggs. So we use the binomial probability distribution to solve this question.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

In which
`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

And p is the probability of X happening.

The expected value of the binomial distribution is:

`E(X) = np`

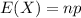
The variance of the binomial distribution is:

`V(X) = np(1-p)`

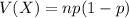
There are 6 eggs

So
`n = 6`

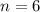
The probability that no eggs are broken is 0.4.

This means that
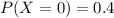`P(X = 0) = 0.4`. So

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 0) = C_(6,0).p^(0).(1-p)^(6)`

`(1 - p)^(6) = 0.4`

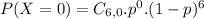
Taking the sixth root from both sides of the equality

`(1 - p) = 0.8584`

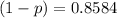
p = 0.1416

Each egg has a 0.1416 probability of being broken

(a) Write out the pmf of X.

Probability of each value, from 0 to 6

`P(X = 0) = C_(6,0).(0.1416)^(0).(0.8584)^(6) = 0.4`

`P(X = 1) = C_(6,1).(0.1416)^(1).(8584)^(5) = 0.3960`

`P(X = 2) = C_(6,2).(0.1416)^(2).(8584)^(4) = 0.1633`

`P(X = 3) = C_(6,3).(0.1416)^(3).(8584)^(3) = 0.0359`

`P(X = 4) = C_(6,4).(0.1416)^(4).(8584)^(2) = 0.0044`

`P(X = 5) = C_(6,5).(0.1416)^(5).(8584)^(1) = 0.0003`

`P(X = 6) = C_(6,6).(0.1416)^(6).(8584)^(0) = 0.00001`

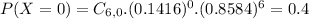
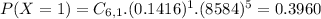
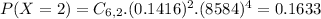
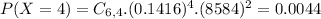
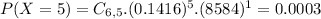
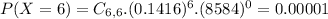
(b) Compute the probability that an even number of eggs is broken.

0, 2, 4 or 6

`P = P(X = 0) + P(X = 2) + P(X = 4) + P(X = 6) = 0.4 + 0.1633 + 0.0044 + 0.00001 = 0.5677`

56.77% probability that an even number of eggs is broken.

(c) Compute the expectation and variance of X.

Expectation:

`E(X) = np = 6*0.1416 = 0.8496`

Variance:

`V(X) = np(1-p) = 6*0.1416*0.8584 = 0.7293`