Answer:
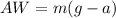 (1)
(1)
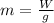 (2)
(2)
 (3)
(3)
And we know from the info given that:
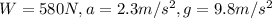
And replacing into equation (3) we got:
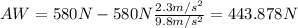
So then we can conclude that the scale will read 443.878 N for Florence
Step-by-step explanation:
For this case we have an accelerator moving downward with an acceleration a.
On this case the person fell like the weight is less than the normal since the required force on the elevator floor is lower than the normal force, for this reason the body accelerate downward.
We can use the formula of apparent weight given by:
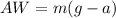 (1)
(1)
Where AW represent the apparent weigth of the person in the elevator
We also know that the weigth is defined as:
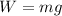
If we solve for m we got:
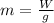 (2)
(2)
If we replace equation (2) into equation (1) we got:
 (3)
(3)
And we know from the info given that:
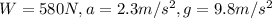
And replacing into equation (3) we got:
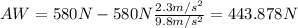
So then we can conclude that the scale will read 443.878 N for Florence