Question

Let f(x)= x(2x-3)/(x+2)x. Find the domain, vertical and horizontal asymptote

Answer 1

Explanation:

Domain of a rational function is everywhere except where we set vertical asymptotes. or removable discontinues

Here, we have

`(x(2x - 3))/((x + 2)x)`

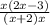
First, notice we have x in both the numerator and denomiator so we have a removable discounties at x.

Since, we don't want x to be 0,

We have a removable discontinuity at x=0

Now, we have

`(2x - 3)/(x + 2)`

We don't want the denomiator be zero because we can't divide by zero.

so

`x + 2 = 0`

`x = - 2`

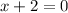
So our domain is

All Real Numbers except-2 and 0.

The vertical asymptors is x=-2.

To find the horinzontal asymptote, notice how the numerator and denomator have the same degree. So this mean we will have a horinzontal asymptoe of

The leading coeffixent of the numerator/ the leading coefficent of the denomiator.

So that becomes

`(2)/(1) = 2`

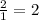
So we have a horinzontal asymptofe of 2