Question

What is the answer to the question

Answer 1

The equation of the parallel line is y = –2x – 11.

Solution:

Given equation of the line is y = –2x – 5.

Slope of this line is
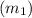`(m_1)` = –2

To write the equation parallel to this line and passes through (–4, –3).

If two lines are parallel, then they have the same slope.

`\Rightarrow m_1=m_2`

`\Rightarrow m_2 =-2`

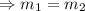
Point-slope formula:

`y-y_1=m(x-x_1)`

Substitute the given values in the formula, we get

`y-(-3)=-2(x-(-4))`

`y+3=-2(x+4)`

`y+3=-2x-8`

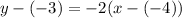
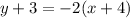
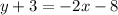
Subtract 3 from both sides of the equation.

`y+3-3=-2x-8-3`

`y=-2x-11`

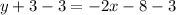
Hence the equation of the parallel line is y = –2x – 11.