Question

For an integer $n$, the inequality

\[x^2 + nx + 15 < 0\]has no real solutions in $x$. Find the number of different possible values of $n$.

Answer 1

We consider the graph of

\[y = x^2 + nx + 15,\]where $n$ is some constant. The graph is an upward-opening parabola, and the solutions of $x^2 + nx +15<0$ correspond to values of $x$ for which this parabola is below the $x$-axis. The parabola only goes below the $x$-axis if the quadratic $x^2 + nx + 15$ has two distinct roots. Otherwise, the parabola does not go below the $x$-axis. So, the inequality $x^2 + nx + 15<0$ has no solutions if and only if the quadratic $x^2+nx + 15$ does not have two distinct roots.

The quadratic $x^2 + nx + 15$ fails to have two distinct roots only when its discriminant, which is $n^2 - 4(1)(15)$, is nonpositive. So, we must have $n^2 - 60 \le 0$, or $n^2 \le 60$. This inequality holds for $-\sqrt{60} \le n \le\sqrt{60}$. Therefore, the integers $n$ for which $x^2 + nx + 15 < 0$ has no real solutions $x$ are the integers from $-7$ up to 7. There are $\boxed{15}$ such integers.

Answer 2

There are 15 different possible values of n:

{-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,7}

Explanation:

The given inequality is

`{x}^(2) + nx + 15 \: < \: 0`

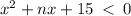
For to have no solution, the discriminant must be less than zero.

This means that:

`{n}^(2) - 4 * 1 * 15 \: < \: 0`

`{n}^(2) - 60 \: < \: 0`

`{(n} - 4 √(15) )(n + 4 √(15) ) \: < \: 0`

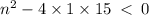
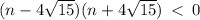
This implies that:

`- 7.75 \: < \: n \: < \: 7.75`

The integer values are , {-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,7}