Explanation:
FORMATION OF TABLE FOR THE FUNCTION
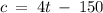
As t represents the temperature in degrees Fahrenheit and c represents the number of cricket chirps per minute.
Considering the function
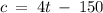
when
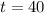
then
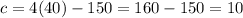
when
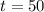
then
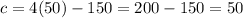
when

then
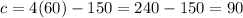
when
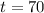
then
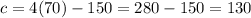
when

then
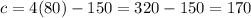
when
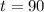
then
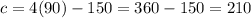
when
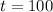
then
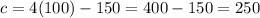
So
Lets form the data table for this function based on the determined values
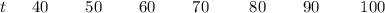
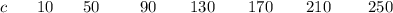
PART 1)
Considering the function
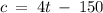
As we know that
when

then
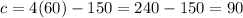
- Meaning the number of chirps per minute would increase to
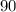 , when the temperature t in degrees Fahrenheit increase to 60.
, when the temperature t in degrees Fahrenheit increase to 60.
The appropriate logic is that the speed at which cricket chirps is based on the temperature. The table table also indicates that as the temperature t increases, the number of cricket chirps also increases.
PART 2)
- A rate of change is a rate that determines how one quantity changes in relation to another quantity.
Considering the two points
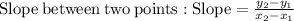
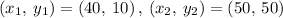
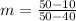
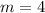
It logically means for every increase of
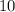 units in
units in
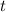 (temperature in degrees Fahrenheit), the value of
(temperature in degrees Fahrenheit), the value of
 (number of chirps) is increasing to
(number of chirps) is increasing to
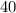 units.
units.
Thus, the rate of change will be
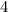 .
.
Part 3)
Considering the function
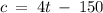
The data table for this function
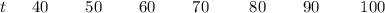
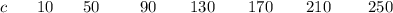
Putting
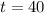 in the function brings the value of
in the function brings the value of
 as
as
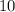 .
.
i.e.
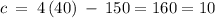
Yes, it does make sense.
Its logical meaning is that at the start, when the value of
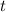 was
was
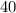 temperature in degrees Fahrenheit, then the value of
temperature in degrees Fahrenheit, then the value of
 (number of chirps per minute) was
(number of chirps per minute) was
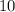 .
.