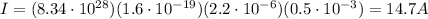Question

A 14-gauge copper wire has a diameter of 1.676 mm. What magnitude current flows in amperes when the drift velocity is 0.500 mm/s? (The density of free electrons in copper is 8.34 ✕ 1028 e−/m3.).)

Answer 1

14.7 A

Step-by-step explanation:

The magnitude current flowing in a conductor is given by

`I=(Q)/(t)`

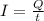
where

Q is the total charge

t is the time interval

The total charge passing through a point in the conductor can be written as

`Q=neAd`

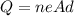
where

n is the density of free electrons

A is the cross-sectional area of the conductor

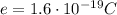`e=1.6\cdot 10^(-19)C` is the electron charge

d is the length of the conductor

The time interval can be written as

`t=(d)/(v_d)`

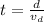
where

d is the length of the conductor

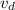`v_d` is the drift velocity of the electrons

Re-arranging the three equations, we get:

`I=(neAd)/(d/v_d)=neAv_d`

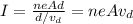
For the copper wire here we have:

`v_d = 0.500 mm/s = 0.5\cdot 10^(-3) m/s`

`n=8.34\cdot 10^(28) m^(-3)`

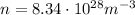
The diameter is 1.676 mm, so the area is

`A=\pi ((d)/(2))^2=\pi ((1.676\cdot 10^(-3))/(2))^2=2.2\cdot 10^(-6)m^2`

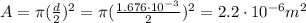
So, the current in the wire is

`I=(8.34\cdot 10^(28))(1.6\cdot 10^(-19))(2.2\cdot 10^(-6))(0.5\cdot 10^(-3))=14.7 A`