Question

The gestation time for humans has a mean of 266 days and a standard deviation of 25 days. If 200 women are randomly selected, find the probability that they have a mean pregnancy between 266 days and 268 days.

Answer 1

The probability that 200 women have a mean pregnancy between 266 days and 268 days is 0.371.

Step-by-step explanation:

Let X = gestation time for humans.

The mean of the random variable X is: E (X) = μ = 266 days.

The standard deviation of the random variable X is: SD (X) = σ = 25 days.

**Assume that the gestation time for humans follows a Normal distribution.

The z-score for the sample mean is:
`z=(\bar x-\mu)/(\sigma/ √(n))`.

The sample of women selected is: n = 200.

Compute the probability that 200 women have a mean pregnancy between 266 days and 268 days as follows:

`P(266\leq \bar X\leq \leq 268)=P((266-266)/(25/ √(200))\leq (\bar X-\mu)/(\sigma/ √(n))\leq (268-266)/(25/ √(200)))\\=P(0\leq Z\leq 1.13)\\=P(Z<1.13)-P(Z<0)\\=0.871-0.50\\=0.371`

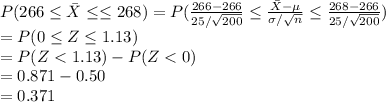
**Use the z-table for the probability.

Thus, the probability that 200 women have a mean pregnancy between 266 days and 268 days is 0.371.