Question

"How did you program your robot to move in a perfect triangle?" Arianna asks, sounding impressed. "It always comes back to exactly where it started!" "My code uses the law of cosines and the law of sines." Raphael proudly replies. "For example, if it moves 3 m3\text{ m}3 m, turns 120?120^\circ120?, then moves 4 m4\text{ m}4 m more, it can compute the distance back to where it started as well as the angle it must turn." In Raphael's example, what distance would his robot compute? Do not round during your calculations. Round your final answer to the nearest hundredth of a meter

Answer 1

The distance computed is 6.08 m

Explanation:

One of the sides (a) of the triangle has a length of 3 m, the other side (b) has a length of 4 m, and the angle (C) form between them measures 120°. The law of cosine states:

c² = a² + b² - 2ab cos C

Replacing with data (dimensions are omitted):

c² = 3² + 4² - 2(3)(4) cos 120°

c = √37

c = 6.08 m

Answer 2

Explanation:

In Raphael's example, the robot moves in a perfect triangle. A perfect triangle is known to have three equal sides and three equal angles of 60° each. Raphael's example mentions the length of two sides of the triangle as 3m and 4m and it also mentions the angle the robot turns 120°

Therefore the angle created is 180°-120°= 60° which is an angle of a perfect triangle.

The distance that the robot has to calculate would be equal to the length of the third side of the triangle

lets assume the length of the third side of the triangle to be
`\beta` and the two remaining angles to be a and b.

To get the distance
`\beta`, let's list out what we know about this triangle.

side a = 3m

side b = 4m

side c = β

Angle 1 = Angle made between side 2 and 3 = A

Angle 2 = Angle made between side 1 and 3 = B

Angle β = Angle made between side 1 and 2 = 60°

The law of cosines states that

`\beta ^(2)` =
`a^(2)` +
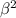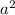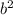`b^(2)` - 2ab(cosβ)

`\beta ^(2)` =
`3^(2)` +
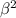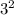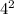`4^(2)` - 2×3×4(cos 60)

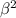`\beta ^(2)` = 9 + 16 - 24(0.5)

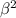`\beta ^(2)` = 9 + 16 - 12

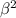`\beta ^(2)` = 13

β =
`√(13)`

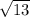
β = 3.6055512755 m

The distance the robot will compute is 3.61 meter to the nearest hundredth.