Question

The volume of a sphere whose diameter is 18 centimeters is _ cubic centimeters. If it’s diameter we’re reduced by half, it’s volume would be _ of its original volume

Answer 1

First Part

Given that

`Volume = (4)/(3) \pi r^(3)`

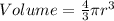
We have that

`Volume = (4)/(3) \pi r^(3) = (4)/(3) \pi ((Diameter)/(2))^(3) = (4)/(3) \pi 9^(3) = 972\pi cm^(3) \approx 3053.63 cm^(3)`

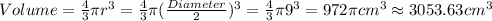
Second Part

Given that

`Volume = (4)/(3) \pi r^(3)`

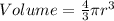
If the Diameter were reduced by half we have that

`Volume = (4)/(3) \pi r^(3) = (4)/(3) \pi ((r)/(2)) ^(3) = ((4)/(3) \pi r^(3))/(8)`

This shows that the volume would be
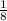`(1)/(8)` of its original volume

Explanation:

First Part

Gather Information

`Diameter = 18cm`

`Volume = (4)/(3) \pi r^(3)`

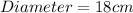
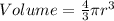
Calculate Radius from Diameter

`Radius = (Diameter)/(2) = (18)/(2) = 9`

Use the Radius on the Volume formula

`Volume = (4)/(3) \pi r^(3) = (4)/(3) \pi 9^(3)`

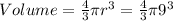
Before starting any calculation, we try to simplify everything we can by expanding the exponent and then factoring one of the 9s

`Volume = (4)/(3) \pi 9^(3) = (4)/(3) \pi 9 * 9 * 9 = (4)/(3) \pi 9 * 9 * 3 * 3`

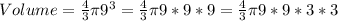
We can see now that one of the 3s can be already divided by the 3 in the denominator

`Volume = (4)/(3) \pi 9 * 9 * 3 * 3 = 4 \pi 9 * 9 * 3`

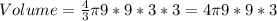
Finally, since we can't simplify anymore we just calculate it's volume

`Volume = 4 \pi 9 * 9 * 3 = 12 \pi * 9 * 9 = 12 * 81 \pi = 972 \pi cm^(3)`

`Volume \approx 3053.63 cm^(3)`

Second Part

Understanding how the Diameter reduced by half would change the Radius

`Radius =(Diameter)/(2)\\\\If \\\\Diameter = (Diameter)/(2)\\\\Then\\\\Radius = ((Diameter)/(2) )/(2) = ((Diameter)/(2))/((2)/(1)) = (Diameter)/(2) * (1)/(2) = (Diameter)/(4)`

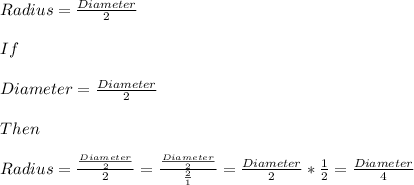
Understanding how the Radius now changes the Volume

`Volume = (4)/(3)\pi r^(3)`

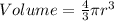
With the original Diameter, we have that

`Volume = (4)/(3)\pi ((Diameter)/(2)) ^(3) = (4)/(3)\pi (Diameter^(3))/(2^(3))\\\\ = (4)/(3)\pi (Diameter^(3))/(2 * 2 * 2) = (4)/(3)\pi (Diameter^(3))/(8)\\\\`

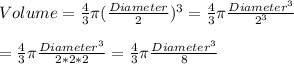
If the Diameter were reduced by half, we have that

`Volume = (4)/(3)\pi ((Diameter)/(4)) ^(3) = (4)/(3)\pi (Diameter^(3))/(4^(3))\\\\ = (4)/(3)\pi (Diameter^(3))/(4 * 4 * 4) = (4)/(3)\pi (Diameter^(3))/(4 * 2 * 2 * 4) = (4)/(3)\pi (Diameter^(3))/(8 * 8) = ((4)/(3)\pi(Diameter^(3))/(8))/(8)`

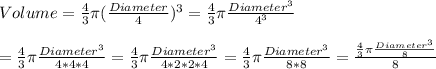
But we can see that the numerator is exactly the original Volume!

This shows us that the Volume would be
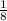`(1)/(8)` of the original Volume if the Diameter were reduced by half.